2003. 10. 25
(1) 特殊種目導入方法の検討今回、従来の五輪種目の距離(一部五輪種目でない)に加えて、五輪種目にない特殊種目(60m、1000mや2マイル、100kmなど)も選択距離に加えることにしました。この計算式では、各々の距離で基準タイムを設定し、その基準タイムを元に計算していますが、その基準タイムは下記表1に示すようになっています。
| 距離 | 持久力レベル9での基準タイム |
| 100m | 10.00 |
| 200m | 20.00 |
| 400m | 44.40 |
| 800m | 1:43.50 |
| 1500m | 3:32.00 |
| 3000m | 7:34.00 |
| 5000m | 13:07.00 |
| 10000m | 27:20.00 |
| ハーフマラソン | 1:00:30 |
| 30km | 1:28:20 |
| マラソン | 2:08:00 |
表1 各距離での基準タイム |
この基準タイムは、持久力レベルが9(世界トップレベル)のときに、100mの10秒00に各種目のレベルが一致するように設定したものですが、世界記録の変遷などを考慮して人為的に設定したタイムです。では、今度新たに加える特殊種目もそのように人為的に定めれば良いかというと、ちょっと問題があります。何故かというと、五輪種目と特殊種目では出された記録を同等に扱えないからです。普段実施される種目は圧倒的に五輪種目が多いです。実施される頻度が高ければ、それだけ良いコンディションで走れる機会も高まるわけで、選手のポテンシャルが最大限引き出された記録が出される確率も高くなるでしょう。ところが、年に1、2回しか実施されないような特殊種目では、そのとき選手のコンディションが良くなかったり、ペース配分が悪かったり、天候が悪かったりしたらそれで終わりです。そういうデータを元にして設定した基準タイムは、信頼性に欠けるということになります。
ところが、ここで良い方法がありました。五輪種目の各距離をその基準タイムで割った値、すなわち基準速度とその距離を、速度を縦軸に、距離を対数軸の横軸にとってプロットし、それらを線で結ぶと、図1のようなきれいな関係があることがわかります。ちなみに、このグラフはMicrosoftの定番表計算ソフト、Excelを使って描き、プロット間の線にはスムージングをかけています。特殊種目の基準速度はこの線上にあり、その特殊種目の距離での基準速度をこのグラフから求め、その速度から逆算すれば、基準タイムを出せる訳です。
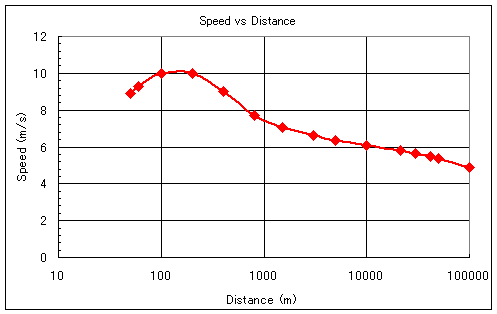 |
図1 基準タイムを元にした速度と距離の関係 (ロスタイム0.0秒) |
さて、従来基準タイムがあった種目に挟まれている距離では、上記方法により基準タイムを求められますが、これらの種目に挟まれていない距離ではそれはできません。そこで、室内で良く実施されている60mについては、室内の記録一覧と屋外の100mの記録、出した選手などを比較して100mの10秒00に相当する基準タイムは6秒45としました。また、100kmについては、10km
― ハーフ ―
マラソンと繋がる一連の直線に近い関係の延長線上を基本にしながら、安部友恵選手(女子100km世界最高記録保持者)のマラソン/100kmの持ちタイムの比較などをしてその記録が非現実的かどうか判断して、基準タイムを5時間40分としました。
(ちなみに、現在の100kmの世界最高は、男子は6時間13分33秒/砂田 貴裕、女子は6時間33分11秒/安部友恵)
(2) 曲線の補正
ところで、このグラフでひとつ困ったことがあります。グラフの大半は直線に似た関係があるのに、100mと200mの速度が同じになっているため、ここで直線に近い関係が崩れてしまっていて、更にその間に曲線の山ができてしまっていて、この間での数値の正確性が低くなってしまいます。さて五輪/世界選手権では100mの勝者のことを世界一速い男と呼んでいるのに、この速度関係からは必ずしもそうなっておらず、実際、現在の世界記録は単純な速度関係では200m(19.32;10.35m/s)の方が100m(9.78;10.22m/s)を上回っており、これでは200mの勝者の方を世界一速い男と呼んでしまっても不思議ではありません。まあ、これは皆さんおわかりのとおり理由は単純で、スタートするときは、リアクションタイムでまず0.1〜0.15秒ロス(0.1秒以内に反応すると、フライングにより失格だから、それより早いことはあり得ない)があり、更に加速でトップスピードに乗るまでのロスがあります。これらの合計がどれくらいか正確にはわかりませんが、4継やマイルリレーとフラットレースとの関係から1.0秒とすると図2のようになり、100mの方が速くなり100mと200mの間に曲線の山ができてしまうという事態は避けられましたが、今度は60mと100mの間に山ができてしまいました。
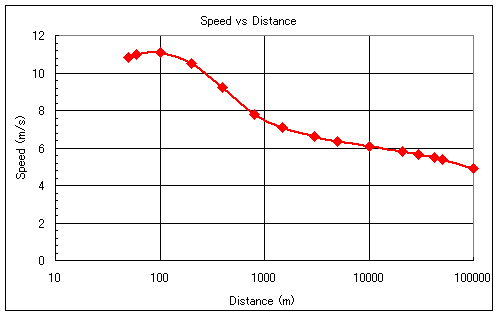 |
図2 基準タイムを元にした速度と距離の関係 (ロスタイム1.0秒) |
さて、ここら更に話を発展させます。どうせなら、せっかく曲線のカーブが緩くなったのなら更にそれを進めて、曲線部分をなくしてしまえということです。実際にはスタートからのロスが2秒などということはあり得ませんが、ここでロスを2.1秒としたところ、図3のように60mから800mあたりまでの関係がほぼ直線関係となりました。これにより、50mの基準タイムを設定するときも、その設定タイムがその直線の延長線上にあれば良いことになり、これで50mについては5秒62というタイムが導き出されました。ロスタイムと2.1秒というところにどうも違和感を感じる方は、この2.1秒は単なる補正係数だと考えてください。
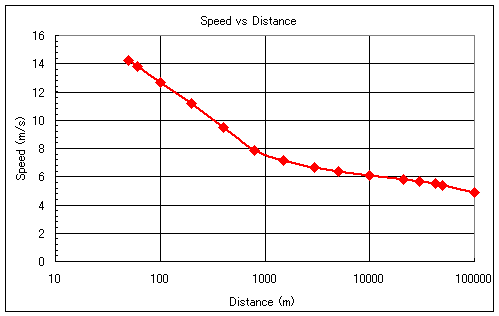 |
図3 基準タイムを元にした速度と距離の関係 (ロスタイム2.1秒) |
(3) 特殊種目の基準タイムの求め方
補正係数2.1秒の導入により、速度と距離の対数との関係が、800m付近を境に直線を折り曲げたようなきれいな形にすることができました。この速度を補正速度と呼ぶことにします。特殊種目の基準タイムはこのグラフから、その種目の距離での補正速度を読み取り、その値から基準タイムを算出すればいい訳ですが、このグラフそのままでは大雑把な値しか読み取れません。そこで、横軸上の求める距離の位置を縦軸と一致させるという工夫をします。そうすれば、グラフと縦軸との交点が補正速度ということになります。Excelでは、グラフの目盛の最小値と最大値を指定できますから、横軸の最小値に求める距離の値を、最大値にそれより大きな適当な値を指定すれば良い訳です。ところがここで問題があります。Excelでは、リニアな軸については最小/最大値に任意の値を指定することができますが、対数軸に関しては10のべき乗(1、10、100、・・・など)しか指定できません。そこで、今度は距離を任意の値で指定できるように工夫します。距離に対して10を底とした対数をとると10mは1、100mは2、・・・10000mは4となり、図4のようなグラフとなり、図3と全く同じようなグラフになります。ここで、今度は10を底とした求める距離の対数をこのグラフの横軸の目盛の最小値に指定すれば、補正速度が求められる訳です。
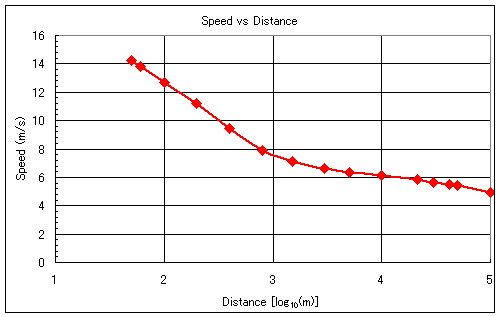 |
図4 基準タイムを元にした速度と、距離の対数との関係 (ロスタイム2.1秒) |
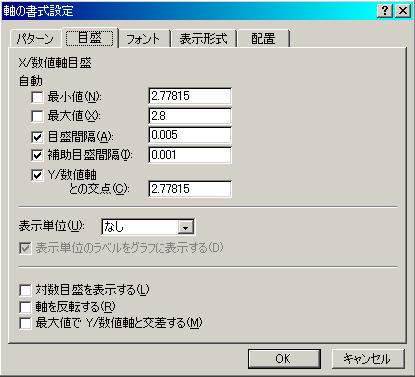 |
図5 Excel横軸目盛の設定 (600mの対数) |
では、具体的にある距離の補正速度、および基準タイムを求めてみます。例として600mについて求めてみると、600mの10を底とした対数は、log10(600) = 2.77815
となりますから、これを横軸の最小値に指定します。横軸の最大値は例えば2.8とします。これだけでも図6から補正速度8.5程度であることがわかりますが、これでは大雑把過ぎます。そこで補正速度が8から9の間にあることはわかりますから、縦軸の最小/最大をそれぞれ8と9を指定します。すると図7のようになり、補正速度が8.48ぐらいあることがわかりました。そこで更に縦軸の最小/最大をそれぞれ8.4と8.5としていすると図8のようになり、補正速度が8.484であることがわかります。この作業を更に詰めると更に細かい値が求められそうですが、あまり細かくするとなぜかグラフの線が別の所にいってしまうという現象が起きてしまうので、ここでこの作業は止めます。値の精度はこれで十分でしょう。補正速度が8.484ですから、基準タイム
= 距離/補正速度 + 補正係数 という式により
600mの基準タイム ; 600/8.484 + 2.1 = 72.82136秒 → 1分12秒82
となります。同じ方法により、基準タイムが設定されている距離の間にある、あらゆる任意の距離について基準タイムを求めることができます。そして、その方法により新たに基準タイムを求めた距離を含めた新しい基準タイム一覧が、表2となります。距離としては、普段の試合ではあまり実施されないけれども、何らかの試合で実施されたことがある距離(例えば150m、300m、1000mなど)を取り上げました。また、ヤード、マイルについては、現在1マイルレースを除いてほとんど実施されませんが、1970年代はじめまでは、100ヤード、2マイル、3マイル、6マイルレースがよく実施されていたので、これらも取り上げました。なお、440ヤード、880ヤードレースなども実施されていましたが、これらはそれぞれ402.34m、804.67mで、あまりにも400m、800mに近すぎる値で意味がないので、取り上げませんでした。これらは単純に、一番近い距離との比率だけで十分です。
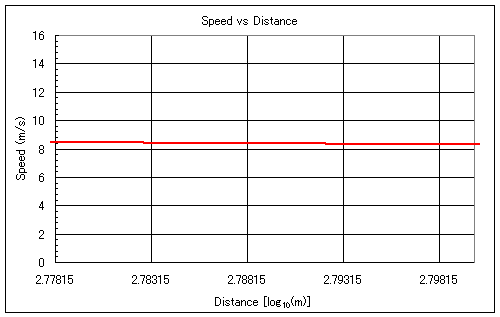 |
図6 600mの対数と縦軸との交点 (縦軸スケールフリー) |
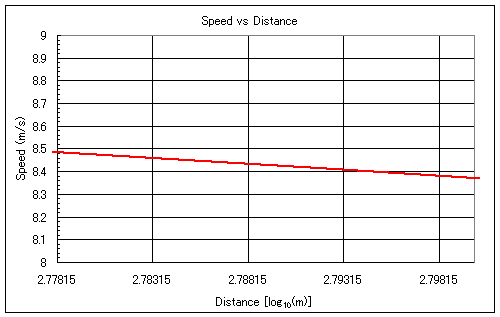 |
図7 600mの対数と縦軸との交点 (縦軸8から9の間へ絞り込み) |
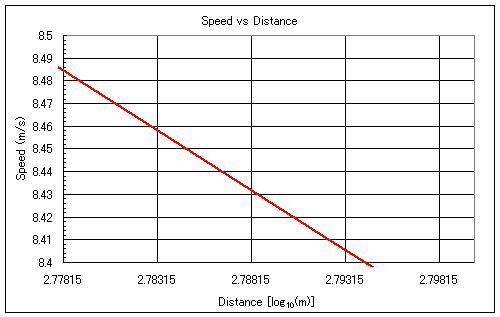 |
図8 600mの対数と縦軸との交点 (縦軸8.4から8.5の間へ絞り込み) |
| 距離 | 持久力レベル9での基準タイム | 設定方法 |
| 100m | 10.00 | 人為 |
| 200m | 20.00 | 人為 |
| 400m | 44.40 | 人為 |
| 800m | 1:43.5 | 人為 |
| 1500m | 3:32.0 | 人為 |
| 5000m | 13:07 | 人為 |
| 10000m | 27:20 | 人為 |
| ハーフマラソン | 1:00:30 | 人為 |
| マラソン | 2:08:00 | 人為 |
| 50m | 5.62 | 人為 |
| 60m | 6.45 | 人為 |
| 150m | 14.81 | 計算 |
| 300m | 31.60 | 計算 |
| 500m | 58.17 | 計算 |
| 600m | 1:12.82 | 計算 |
| 1000m | 2:14.41 | 計算 |
| 2000m | 4:51.54 | 計算 |
| 3000m | 7:34.0 | 人為 |
| 15km | 42:03.5 | 計算 |
| 20km | 57:08.5 | 計算 |
| 30km | 1:28:20 | 人為 |
| 50km | 2:34:30 | 人為 |
| 100km | 5:40:00 | 人為 |
| 100 yards (91.44m) | 9.214 | 計算 |
| 1 mile (1609.34m) | 3:49.34 | 計算 |
| 2 miles (3218.68m) | 8:10.22 | 計算 |
| 3 miles (4828.02m) | 12:38.1 | 計算 |
| 6 miles (9656.04m) | 26:20.4 | 計算 |
| 10 miles (16093.4m) | 45:19.7 | 計算 |
表2 特殊種目も含めた基準タイム一覧 |
(4) 終わりに
今回、普段実施されない種目についても基準タイムを求め、その種目についてもレベルの比較ができるようになりました。この計算式により、つい先日私が1000mで3分を切りましたが、その記録2分56秒94を入れて計算してみたところ、この記録に相当する800mの記録は、持久力レベルが「大学同好会レベル」
の5で2分16秒37、「世界トップレベル」の9で2分16秒76となり、自分が当初思っていた2分14〜15秒というレベルよりも低く、ちょっとがっかりしてしまいました。この計算式で計算してみて、自分の感覚と違うと感じた人も多いかもしれません。例えば800mについて考えてみると、私の800mの
ベストは2分09秒34ですから、それに相当するレベルの600mのタイムは1分31秒台となりますが、実際には1分37秒台でしか走ったことがありません。あま、これは極端な例でしょうが、このような人は多いと思います。
自分の感覚と計算式でのタイムとのズレは、最大限の力を出せるように練習/調整をしていて、更に本番では競り合う相手など様々なプラス要因が上乗せされる試合のタイムに対し、そのようなプラス面のない練習のタイムとの違いの差でしょう。この計算式は、データの多い一般種目(五輪種目)の基準タイムを元に、グラフから客観的に正確に導き出したものですから、おそらく本人が思っている感覚よりは、こちらのタイムの方が正しいという確信があります。逆にいうと、こういう特殊種目でも試合などの機会が与えられ、それに向けてじっくり調整して臨めばそういうタイムを出せるという指針になるのではないでしょうか?
もしこれからこういう種目を走られる機会がある方は、この計算式を元に目標タイムを立てられてみてはどうでしょうか?
(*)私の場合、1人で走っていること、疲労がやや残っている状態で走っていたこと、この後2本走るので無意識のうちにペースをセーブしていたかもしれないこと、更に社会人になってからの400mのベストが58秒台と悪く、相対的に持久型ランナーになってしまったため、600mも800mに比べて相対的に遅くなっていることなどが原因だと思います。